viernes, 11 de abril de 2008
SOLUCION DE ECUACIONES DIFERENCIALES
El trabajo sobre ecuaciones diferenciales, método de Rounge-Kutta, Euler, se encuentran en la siguiente dirección: http://muyametodosnumericos.scienceontheweb.net/ROUNGE-KUTTA-EULER.rar
jueves, 6 de marzo de 2008
APROXIMACIONES
1.-escribir un programa para aproximar por una recta un conjunto de datos por le método de los mínimos cuadrados. Incluir en dicho programa, la grafica de la recta, grafica del conjunto de datos, el coeficiente de correlación r.
SOLUCION
PROGRAMA EN MATLAB PARA APROXIMAR A UNA RECTA.
function correl
xi=input('ingrese los valores de xi:\n');
yi=input('ingreso los valores de yi:\n');
n=length(xi);
A=ones(2);
for i=1:2
for j=1:2
A(i,j)=sum(xi.^(1+i-j));
end
end
B=ones(2,1);
for i=0:1
B(1+i,1)=sum(yi.*xi.^i);
end
X=inv(A)*(B);
l=X(1);r=X(2);
fprintf('\nLos coeficientes de la ecuacion son:\n')
fprintf(' a b\n')
fprintf('%8.5f%10.5f\n',l,r)
y=l*xi+r;
m=sum(yi)/n;
t=sum((yi-y).^2);
j=sum((yi-m).^2);
r2=1-(t/j);
z=(r2)^0.5;
fprintf('\n El coeficiente de determinacion r^2=');
fprintf('%5.5f\n',r2);
if(l>0)
fprintf('\n El coeficiente de correlacion r=');
fprintf('%5.5f\n',z);
else
fprintf('\n El coeficiente de correlacion r=');
fprintf('%5.5f\n',-z);
end
x1=xi;
x1=sort(x1);
x1=x1(1):0.001:x1(n);
p=polyval(X,x1);
plot(xi,yi,'m.',x1,p),grid on
2.-hallar la recta por el método de los mínimos cuadrados que se ajusten mejor al conjunto de datos. Escribir las ecuaciones normales.
xi 4 5 2 5 6 7 1 8 3 7
yi 5 6 4 5 7 10 3 11 4 9
SOLUCION
Empleando el programa de la pregunta 1.
Graficando:
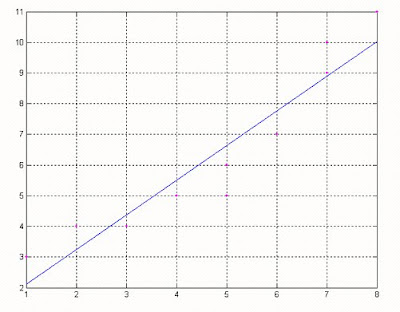
y los resultados de la ecuación de la recta y su coeficiente de correlación son:
correl
ingrese los valores de xi:
[4 5 2 5 6 7 1 8 3 7]
ingreso los valores de yi:
[5 6 4 5 7 10 3 11 4 9]
Los coeficientes de la ecuacion son:
a b
1.13025 0.97479
El coeficiente de determinacion r^2=0.88900
El coeficiente de correlacion r=0.94287
3.-dado el conjunto de datos:
xi Yi
0.15 4.4964
0.40 5.1284
0.60 5.6931
1.01 6.2884
1.50 7.0989
2.20 7.5507
2.4 7.5106
2.70 8.0756
2.90 7.8708
3.50 8.2408
3.80 8.5303
4.40 8.7394
4.60 8.9981
5.10 9.1450
6.60 9.5070
7.60 9.9115
Se ajusta a la función y=bx^a.
a).-linealizar y=bx^a y modifique el programa de mínimos cuadrados para obtener esta función.
b).- hacer en la misma pantalla grafica de la función en el plano xy y la grafica en el plano log(x) log(y)).
SOLUCION.
a.- linealizando se tiene:
ln(y)=ln(b)+a*ln(x),
Luego para que sea lineal
y=a1*x+b1
Entonces:
a1=a; b1=b; ln(y)=y; ln(x)=x.
Modificando el programa en matlab para estas expresiones: se ha guardado con el nombre de “bxn”.
bxn
ingrese los valores de xi:
[0.15 0.40 0.6 1.01 1.5 2.2 2.4 2.7 2.9 3.5 3.8 4.4 4.6 5.1 6.6 7.6]
ingreso los valores de yi:
[4.4964 5.1284 5.6931 6.2884 7.0989 7.5507 7.5106 8.0756 7.8708 8.2403 8.5303 8.7394 8.9981 9.1450 9.5070 9.9115]
Los coeficientes de la ecuacion son:
a b
0.20935 6.41575
La función y=6.41875*x^0.20935
El coeficiente de determinacion r^2=0.99314
El coeficiente de correlación r=1.85876
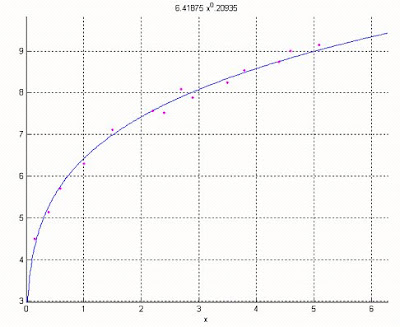
4.- escribir un programa para aproximar por polinomio P(x) de grado k un conjunto de datos por el método de los mínimos cuadrados, incluir en dicho programa la grafica del polinomio, grafica del conjunto de datos el coeficiente de correlación.
PROGRAMA PARA APROXIMAR A UN POLINOMIO DE GRADO K.
function polinomial
fprintf('\n FUNCION POLINOMIAL \n')
x=input('\n Ingrese los valores de xi :\n');
y=input('\n Ingrese los valores de yi :\n');
n=input('\n Ingrese el grado del polinomio:\n');
m=n+1;
A=ones(m);
for i=1:m
for j=1:m
A(i,j)=sum(x.^(n+i-j));
end
end
B=ones(m,1);
for i=0:n
B(1+i,1)=sum(y.*x.^i);
end
Z=(inv(A)*B);
fprintf('los coeficientes del polinomio son:\n');
fprintf('%8.5f\n',Z);
x1=x;
x1=sort(x1);
x1=x1(1):0.001:x1(length(x1));
H=polyval(Z,x1);
S=polyval(Z,x);
L=sum(y)/length(y);
R=sum((y-S).^2);
C=sum((y-L).^2);
K=1-(R/C);
J=K^0.5;
fprintf('El coeficiente de determinacion r^2:\n');
fprintf('%8.5f\n',K);
fprintf('El coeficiente de correlacion r:\n');
fprintf('%8.5f\n',J);
plot(x,y,'r*',x1,H),grid on
5.- Obtener la parábola por el método de los mínimos cuadrados que se aproxime ala función f(x)=x^(1/3) en los puntos 1,0,8, ¿Cuáles son las ecuaciones normales, interprete el coeficiente de correlación.
SOLUCION
Debemos aproximar este conjunto de valores a una ecuación de segundo grado.
El conjunto de datos seran:
Xi Yi
-1 -1
0 0
8 2
Empleando el programa polinomial.
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-1 0 8]
Ingrese los valores de yi :
[-1 0 2]
Ingrese el grado del polinomio:
2
los coeficientes del polinomio son:
-0.08333
0.91667
-0.00000
El coeficiente de determinacion r^2:
1.00000
El coeficiente de correlación r:
1.00000
El coeficiente de correlación r es 1, dado que todos los puntos pasan por la ecuación de la parábola
F(x)=-0.0833*x^2+0.91667*x=-1/12*x^2+11/12*x
6.-si una población tiene un crecimiento logístico y no puede superar la cantidad de 1000 individuos entonces el número P de individuos t viene dado por:
P(t)=1000/(1+Ce^At)
Aproxime mediante el método de los mínimos cuadrados, con linealizacion el valor C y A para los siguientes datos:
Xi 0 1 2 3 4
yi 200 300 650 850 950
Solución
Linealizando la función P(x), se tiene:
Ln(1000/y-1)=At+ln(C),
Entonces:
y=ln(1000/y-1); x=x; A=a; C=exp(b)
Modificando el programa de correl se tiene:
ingrese los valores de xi:
[0 1 2 3 4]
ingreso los valores de yi:
[200 400 650 850 950]
Los coeficientes de la ecuación son:
A C
-1.08015 4.30184
7.- considere los puntos {(-2,-3), (-1,-6), (0,-5), (1,1), (2,13)}
a.- determinar el polinomio de grado 3 por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales el coeficiente de correlación
Solución:
Para un polinomio de tercer grado:
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
3
los coeficientes del polinomio son:
0.16667
2.50000
3.33333
-5.00000
El coeficiente de determinacion r^2:
1.00000
El coeficiente de correlación r:
1.00000
Entonces el polinomio de grado tres es:
0.16667*x^3+2.5*x^2+3.3333*x-5.0
b.-determine la parábola por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales el coeficiente de correlación.
Solución
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
2
los coeficientes del polinomio son:
2.50000
3.90000
-5.00000
El coeficiente de determinacion r^2:
0.99833
El coeficiente de correlación r= 0.99917
Entonces la función parabólica es:
Y=2.5*x^2+3.9*x-5
c.- determinar la recta por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales, coeficiente de correlación.
Solución
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
1
Los coeficientes del polinomio son:
3.90000
0.00000
El coeficiente de determinacion r^2:
0.63375
El coeficiente de correlación r:
0.79608
De donde se tiene la recta:
Y=3.9*x
d.- explicar los resultados.
Los puntos dados se ajustan mejor a la un polinomio de tercer grado, dado que todos los puntos pasan por la grafica de la función, así como explica sus coeficientes de correlación, para tercer grado es 1.00 y es la recta la que mejor se aproximan los puntos, por ello su coeficiente de correlación es 0.79608.
SOLUCION
PROGRAMA EN MATLAB PARA APROXIMAR A UNA RECTA.
function correl
xi=input('ingrese los valores de xi:\n');
yi=input('ingreso los valores de yi:\n');
n=length(xi);
A=ones(2);
for i=1:2
for j=1:2
A(i,j)=sum(xi.^(1+i-j));
end
end
B=ones(2,1);
for i=0:1
B(1+i,1)=sum(yi.*xi.^i);
end
X=inv(A)*(B);
l=X(1);r=X(2);
fprintf('\nLos coeficientes de la ecuacion son:\n')
fprintf(' a b\n')
fprintf('%8.5f%10.5f\n',l,r)
y=l*xi+r;
m=sum(yi)/n;
t=sum((yi-y).^2);
j=sum((yi-m).^2);
r2=1-(t/j);
z=(r2)^0.5;
fprintf('\n El coeficiente de determinacion r^2=');
fprintf('%5.5f\n',r2);
if(l>0)
fprintf('\n El coeficiente de correlacion r=');
fprintf('%5.5f\n',z);
else
fprintf('\n El coeficiente de correlacion r=');
fprintf('%5.5f\n',-z);
end
x1=xi;
x1=sort(x1);
x1=x1(1):0.001:x1(n);
p=polyval(X,x1);
plot(xi,yi,'m.',x1,p),grid on
2.-hallar la recta por el método de los mínimos cuadrados que se ajusten mejor al conjunto de datos. Escribir las ecuaciones normales.
xi 4 5 2 5 6 7 1 8 3 7
yi 5 6 4 5 7 10 3 11 4 9
SOLUCION
Empleando el programa de la pregunta 1.
Graficando:

y los resultados de la ecuación de la recta y su coeficiente de correlación son:
correl
ingrese los valores de xi:
[4 5 2 5 6 7 1 8 3 7]
ingreso los valores de yi:
[5 6 4 5 7 10 3 11 4 9]
Los coeficientes de la ecuacion son:
a b
1.13025 0.97479
El coeficiente de determinacion r^2=0.88900
El coeficiente de correlacion r=0.94287
3.-dado el conjunto de datos:
xi Yi
0.15 4.4964
0.40 5.1284
0.60 5.6931
1.01 6.2884
1.50 7.0989
2.20 7.5507
2.4 7.5106
2.70 8.0756
2.90 7.8708
3.50 8.2408
3.80 8.5303
4.40 8.7394
4.60 8.9981
5.10 9.1450
6.60 9.5070
7.60 9.9115
Se ajusta a la función y=bx^a.
a).-linealizar y=bx^a y modifique el programa de mínimos cuadrados para obtener esta función.
b).- hacer en la misma pantalla grafica de la función en el plano xy y la grafica en el plano log(x) log(y)).
SOLUCION.
a.- linealizando se tiene:
ln(y)=ln(b)+a*ln(x),
Luego para que sea lineal
y=a1*x+b1
Entonces:
a1=a; b1=b; ln(y)=y; ln(x)=x.
Modificando el programa en matlab para estas expresiones: se ha guardado con el nombre de “bxn”.
bxn
ingrese los valores de xi:
[0.15 0.40 0.6 1.01 1.5 2.2 2.4 2.7 2.9 3.5 3.8 4.4 4.6 5.1 6.6 7.6]
ingreso los valores de yi:
[4.4964 5.1284 5.6931 6.2884 7.0989 7.5507 7.5106 8.0756 7.8708 8.2403 8.5303 8.7394 8.9981 9.1450 9.5070 9.9115]
Los coeficientes de la ecuacion son:
a b
0.20935 6.41575
La función y=6.41875*x^0.20935
El coeficiente de determinacion r^2=0.99314
El coeficiente de correlación r=1.85876

4.- escribir un programa para aproximar por polinomio P(x) de grado k un conjunto de datos por el método de los mínimos cuadrados, incluir en dicho programa la grafica del polinomio, grafica del conjunto de datos el coeficiente de correlación.
PROGRAMA PARA APROXIMAR A UN POLINOMIO DE GRADO K.
function polinomial
fprintf('\n FUNCION POLINOMIAL \n')
x=input('\n Ingrese los valores de xi :\n');
y=input('\n Ingrese los valores de yi :\n');
n=input('\n Ingrese el grado del polinomio:\n');
m=n+1;
A=ones(m);
for i=1:m
for j=1:m
A(i,j)=sum(x.^(n+i-j));
end
end
B=ones(m,1);
for i=0:n
B(1+i,1)=sum(y.*x.^i);
end
Z=(inv(A)*B);
fprintf('los coeficientes del polinomio son:\n');
fprintf('%8.5f\n',Z);
x1=x;
x1=sort(x1);
x1=x1(1):0.001:x1(length(x1));
H=polyval(Z,x1);
S=polyval(Z,x);
L=sum(y)/length(y);
R=sum((y-S).^2);
C=sum((y-L).^2);
K=1-(R/C);
J=K^0.5;
fprintf('El coeficiente de determinacion r^2:\n');
fprintf('%8.5f\n',K);
fprintf('El coeficiente de correlacion r:\n');
fprintf('%8.5f\n',J);
plot(x,y,'r*',x1,H),grid on
5.- Obtener la parábola por el método de los mínimos cuadrados que se aproxime ala función f(x)=x^(1/3) en los puntos 1,0,8, ¿Cuáles son las ecuaciones normales, interprete el coeficiente de correlación.
SOLUCION
Debemos aproximar este conjunto de valores a una ecuación de segundo grado.
El conjunto de datos seran:
Xi Yi
-1 -1
0 0
8 2
Empleando el programa polinomial.
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-1 0 8]
Ingrese los valores de yi :
[-1 0 2]
Ingrese el grado del polinomio:
2
los coeficientes del polinomio son:
-0.08333
0.91667
-0.00000
El coeficiente de determinacion r^2:
1.00000
El coeficiente de correlación r:
1.00000
El coeficiente de correlación r es 1, dado que todos los puntos pasan por la ecuación de la parábola
F(x)=-0.0833*x^2+0.91667*x=-1/12*x^2+11/12*x
6.-si una población tiene un crecimiento logístico y no puede superar la cantidad de 1000 individuos entonces el número P de individuos t viene dado por:
P(t)=1000/(1+Ce^At)
Aproxime mediante el método de los mínimos cuadrados, con linealizacion el valor C y A para los siguientes datos:
Xi 0 1 2 3 4
yi 200 300 650 850 950
Solución
Linealizando la función P(x), se tiene:
Ln(1000/y-1)=At+ln(C),
Entonces:
y=ln(1000/y-1); x=x; A=a; C=exp(b)
Modificando el programa de correl se tiene:
ingrese los valores de xi:
[0 1 2 3 4]
ingreso los valores de yi:
[200 400 650 850 950]
Los coeficientes de la ecuación son:
A C
-1.08015 4.30184
7.- considere los puntos {(-2,-3), (-1,-6), (0,-5), (1,1), (2,13)}
a.- determinar el polinomio de grado 3 por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales el coeficiente de correlación
Solución:
Para un polinomio de tercer grado:
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
3
los coeficientes del polinomio son:
0.16667
2.50000
3.33333
-5.00000
El coeficiente de determinacion r^2:
1.00000
El coeficiente de correlación r:
1.00000
Entonces el polinomio de grado tres es:
0.16667*x^3+2.5*x^2+3.3333*x-5.0
b.-determine la parábola por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales el coeficiente de correlación.
Solución
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
2
los coeficientes del polinomio son:
2.50000
3.90000
-5.00000
El coeficiente de determinacion r^2:
0.99833
El coeficiente de correlación r= 0.99917
Entonces la función parabólica es:
Y=2.5*x^2+3.9*x-5
c.- determinar la recta por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales, coeficiente de correlación.
Solución
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
1
Los coeficientes del polinomio son:
3.90000
0.00000
El coeficiente de determinacion r^2:
0.63375
El coeficiente de correlación r:
0.79608
De donde se tiene la recta:
Y=3.9*x
d.- explicar los resultados.
Los puntos dados se ajustan mejor a la un polinomio de tercer grado, dado que todos los puntos pasan por la grafica de la función, así como explica sus coeficientes de correlación, para tercer grado es 1.00 y es la recta la que mejor se aproximan los puntos, por ello su coeficiente de correlación es 0.79608.
viernes, 22 de febrero de 2008
SOLUCION DE EJERCICIOS EMPLEANDO MATLAB
Para encontrar las raíces de este tipo de ecuaciones, tenemos los siguientes métodos:
a.- método de la bisección
b.- método del punto fijo
c.- método de newton –Raphson
d.- método de la secante
e.- método de la falsa posición
f.- método de newton modificado
g.- entre otros métodos
1.- METODO DE LA BISECCION
Si se tiene dos puntos x1 y x2 entonces sus correspondiente imágenes son f(x1) y f(x2), lo que se quiere es que estas dos imágenes sean de singo contrario, para que en este intervalo de x1 a x2 se encuentra la raíz buscada. Geométricamente se tiene en la figura 1.
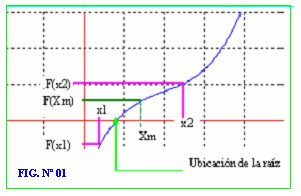
En esta figura 1 se observa que para x1, su imagen f(x1) negativo, para x2 su imagen f(x2) es positivo, entonces en el intervalo [x1, x2], se encuentra la raíz buscada.
Una vez que se ha localizado el intervalo en la cual se encuentra la raíz, solo nos queda
Aproximarnos. Geométricamente se interpreta así.
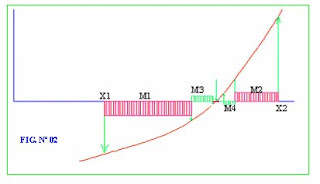
En la figura Nº 02, se ingresa inicialmente X1 y X2, luego se obtiene XM donde M1 corresponde a la mitad del intervalo [X1 X2], a continuación para acercarnos a la raíz.
Tomamos XM=X2 y X2=X2 y se obtiene el nuevo punto medio M2 que corresponde a la mitad del intervalo [XM, X2], y así sucesivamente hasta acercarnos a la raíz
PROGRAMA EN MATLAB PARA EL METODO DE BISECCION
2.- METODO DEL PUNTO FIJOEl método del punto fijo consiste en que a partir de un punto inicial nos acercamos a la raíz buscada, para lo cual se requiere hacer de la función principal f(x) igual a la siguiente expresión: f(x)=x-g(x).
Geométricamente el método del punto fijo consiste en lo siguiente:
Sabemos que existen dos funciones:
y=x,
y=g(x),
Además sabemos que cuando g’(x) <1, entonces el método converge y se puede encontrar la raíz buscada, tal como se muestra en las siguientes figuras Nº 03 y 04
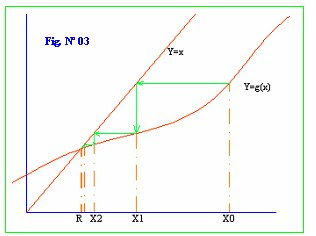
A partir de X0 se llega a la raíz R, cuando esta converge, tal como se observa en la figura Nº 03.
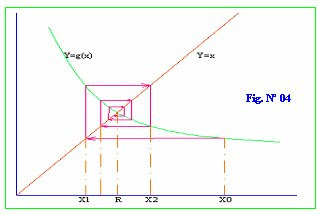
Convergencia oscilatoria, según el número de iteraciones se aproxima a la raíz
PROGRAMA EN MATLAB PARA EL METODO DEL PUNTO FIJO
3.-METODO DE NEWTON RAPHSONEl método consiste en que a partir de un punto dado, la pendiente de la función tiene que converger a la raíz, geométricamente se interpreta de la siguiente manera
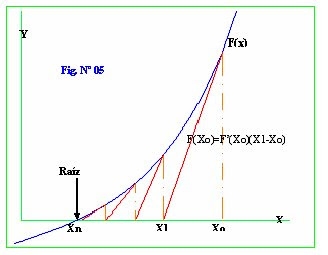
Por lo tanto para determinar la raíz mediante el método de newton es necesario dar valor inicial (X0) adecuada, para que pueda converger rápidamente. Como se observa en la Fig. Nº 05, dado un punto inicial se determina la ecuación de la recta que es tangente a la función en ese punto, luego con esta se determina un X1, que corresponde a la intersección de la ecuación lineal con el eje de las abscisas, con este valor nuevamente se determina la ecuación de la recta tangente a la función, y así sucesivamente nos acercamos a la raíz de la ecuación.
PROGRAMA EN MATLAB PARA EL METODO DE NEWTON RAPHSON
4.- METODO DE LA SECANTE.En el método de la secante no es necesario emplear la derivada de la función, por lo que es uno de los métodos utilizados cuando las derivadas son dificultosas, solo se requiere dos puntos iniciales, estos puntos deben ser dados con criterio para que pueda converger rápidamente.
Geométricamente este método consiste emplear una secante a la función dada.
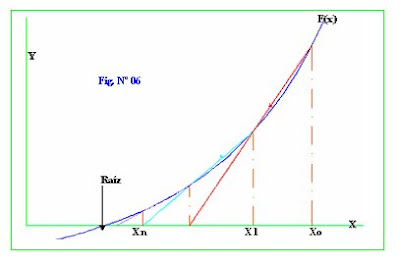
Para este método inicialmente se tiene los puntos Xo y X1, con las correspondientes imágenes de estos dos puntos se determina la ecuación de la recta secante a la función dada, luego esta se intercepta con el eje de las abscisas obteniendo un punto X3, la imagen de X3 para la siguiente iteración es nuevo X1 para definir la secante a la función e interceptar al eje de las abscisas, así nos acercamos cada vez mas hacia a la raíz buscada
PROGRAMA EN MATLAB PARA EL METODO DE LA SECANTE
5.-METODO DE NEWTON MODOFICADOLos criterios que se toman son las tomadas en el método de newton Raspón.
PROGRAMA EN MATLAB PARA EL METODO DE NEWTON MODIFICADO.
6.- METODO DE FALSA POSICIONEl método de la falsa posición también requiere dos puntos iniciales, donde sus correspondientes imágenes deben ser de signos contrarios así como en el método de la bisección, para entender este método se ilustra geométricamente.
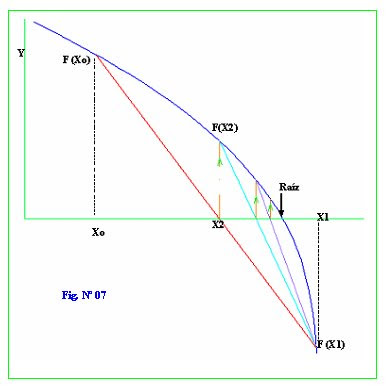
Para los puntos X0 y X1 se determina sus correspondientes imágenes, estos deben ser de signo contrario, así como se muestra en la Fig. Nº 07, se define la ecuación de esta recta, para poder interceptar con el eje de las abscisas, este punto de intersección tiene una imagen que puede ser positivo o negativo, si es positivo como en el grafico que se ilustra x2 es X0 para la siguiente iteración y X1 sigue siendo X1, como se observa cada vez nos acercamos ala raíz. Se continúa con el mismo proceso hasta satisfacer una determinada tolerancia.
PROGRAMA EN MATLAB PARA EL METODO DE FALSA POSICION
EJERCICIOS RESUELTOS
1.-Hallar las raíces de las funciones dadas a continuación intervalos dados y con una precisión de 10^ (-4).
a) x^3-2*x-5=0 en [1, 4]
b) x-0.8-0.2*sin(x)=0 en [0, pi/2]
SOLUCIÓN
a)
Empleando el método de newton.
Para lo cual graficamos inicialmente para aproximar en que punto se encuentra la raíz
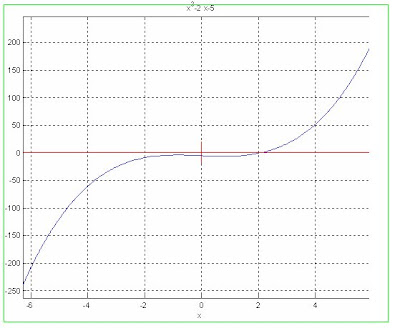
Como se indicaba en la pregunta existe una raíz en ese intervalo, por la tanto:
METODO DE NEWTON:
INGRESE LA FUNCION:
x^3-2*x-5
INGRESE EL PUNTO INICIAL:
1
INGRESE TOLERANCIA:
10^(-4)
it x0 x1 |x1-x0|
1 1.000000000 7.000000000 6.000000000
2 7.000000000 4.765517241 2.234482759
3 4.765517241 3.348702759 1.416814482
4 3.348702759 2.531599641 0.817103118
5 2.531599641 2.173915885 0.357683756
6 2.173915885 2.097883686 0.076032198
7 2.097883686 2.094557716 0.003325971
8 2.094557716 2.094551482 0.000006234
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 2.094551482
b)
Graficando
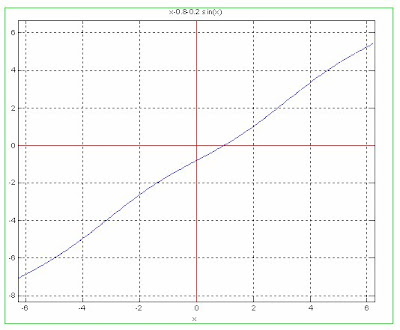
La raíz se encuentra en el intervalo [0,2], entonces.
INGRESE LA FUNCION:
x-0.8-0.2*sin(x)
INGRESE EL PUNTO INICIAL:
>> 0
INGRESE TOLERANCIA:
10^ (-4)
it x0 x1 |x1-x0|
1 0.000000000 1.000000000 1.000000000
2 1.000000000 0.964452968 0.035547032
3 0.964452968 0.964333889 0.000119079
4 0.964333889 0.964333888 0.000000001
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 0.964333888
2.- la función f(x)= (4*x-7)/(x-2) tiene una raíz en p=1.75. Graficar la función f(x). Use el método de newton con los siguientes puntos iniciales.
a) x0=1.625 b) x0=1.875
c) x0=1.5 d) x0=1.95
e) x0=3 f) x0=7 Explique sus resultados.
SOLUCION
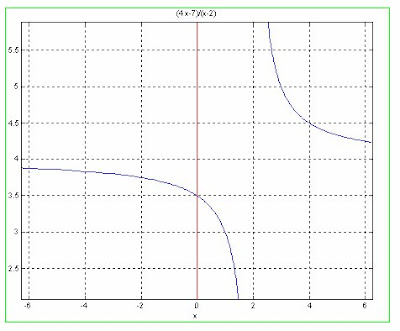
En el grafico de la función se observa que existe una raíz en ese punto, a continuación probaremos con cada uno de los puntos:
Para x0=1.625
INGRESE LA FUNCION:
(4*x-7)/(x-2)
INGRESE EL PUNTO INICIAL:
1.625
INGRESE TOLERANCIA:
10^(-4)
it x0 x1 x1-x0
1 1.625000000 1.812500000 0.187500000
2 1.812500000 1.765625000 0.046875000
3 1.765625000 1.750976563 0.014648438
4 1.750976563 1.750003815 0.000972748
5 1.750003815 1.750000000 0.000003815
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.750000000
Resultados:
X0 Raíz
1.625 1.75
1.875 1.75
1.5 NaN
1.95 1.75
3 NaN
7 NaN
Para los puntos 1.5, 3 y 7, se obtiene como resultado NaN, matlab quiere decir que es u número infinito, dado que en esos puntos la tangente a la función se hacen grandes y divergen de la raíz.
3.- use el método de newton para resolver la ecuación
(sin(x)-x)^2=0 con una presicion de 10^(-5)
a) x0= pi/2
b) x0=5*pi
c) x0=10*pi
SOLUCION
Graficando la función se tiene.
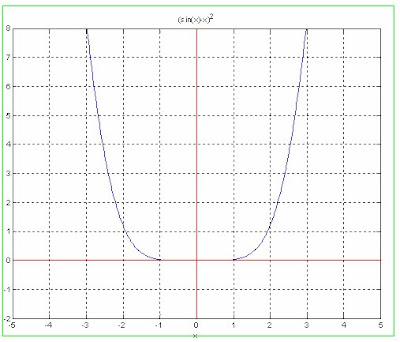
Existe la posibilidad de que haya raíz en el intervalo de [-1 1]. Entonces para cada caso realizamos las iteraciones correspondientes.
INGRESE LA FUNCION:
(sin(x)-x)^2
INGRESE EL PUNTO INICIAL:
pi/2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 1.570796327 1.285398163 0.285398163
2 1.285398163 1.058629574 0.226768589
3 1.058629574 0.875326162 0.183303413
4 0.875326162 0.725607891 0.149718271
5 0.725607891 0.602510190 0.123097701
6 0.602510190 0.500860754 0.101649436
7 0.500860754 0.416679618 0.084181136
8 0.416679618 0.346828593 0.069851025
9 0.346828593 0.288791050 0.058037543
10 0.288791050 0.240525001 0.048266048
11 0.240525001 0.200360036 0.040164965
12 0.200360036 0.166921948 0.033438088
13 0.166921948 0.139075759 0.027846189
14 0.139075759 0.115881511 0.023194248
15 0.115881511 0.096559276 0.019322234
16 0.096559276 0.080461060 0.016098216
17 0.080461060 0.067047989 0.013413071
18 0.067047989 0.055871649 0.011176340
19 0.055871649 0.046558739 0.009312911
20 0.046558739 0.038798388 0.007760351
21 0.038798388 0.032331666 0.006466723
22 0.032331666 0.026942867 0.005388799
23 0.026942867 0.022452281 0.004490586
24 0.022452281 0.018710171 0.003742110
25 0.018710171 0.015591773 0.003118398
26 0.015591773 0.012993123 0.002598650
27 0.012993123 0.010827590 0.002165533
28 0.010827590 0.009022985 0.001804605
29 0.009022985 0.007519150 0.001503835
30 0.007519150 0.006265956 0.001253194
31 0.006265956 0.005221629 0.001044327
32 0.005221629 0.004351356 0.000870272
33 0.004351356 0.003626130 0.000725227
34 0.003626130 0.003021775 0.000604355
35 0.003021775 0.002518145 0.000503629
36 0.002518145 0.002098454 0.000419691
37 0.002098454 0.001748712 0.000349742
38 0.001748712 0.001457260 0.000291452
39 0.001457260 0.001214383 0.000242877
40 0.001214383 0.001011986 0.000202397
41 0.001011986 0.000843322 0.000168664
42 0.000843322 0.000702768 0.000140554
43 0.000702768 0.000585640 0.000117128
44 0.000585640 0.000488033 0.000097607
45 0.000488033 0.000406694 0.000081339
46 0.000406694 0.000338912 0.000067782
47 0.000338912 0.000282427 0.000056485
48 0.000282427 0.000235356 0.000047071
49 0.000235356 0.000196130 0.000039226
50 0.000196130 0.000163441 0.000032688
LA RAIZ BUSCADA ES= 0.000163441
Se observa que requiere muchas iteraciones.
X0 Raíz Número de it
Pi/2=1.700796 0.000163441 50
5*pi=15.707963 0.000507692 50
10*pi=31.4159265 NaN
Si se sigue buscado un punto que satisfaga mejor nuestro búsqueda de raíz seria un numero cercano a cero, dado que la función no corta al eje de la abscisas, solo intercepta en x=0. Se puede observar cuando mas cerca es el punto inicial nos aproximamos la raíz, la raíz buscada con la precisión dada varia de acuerdo al punto inicial. Así para X1= 0.002, la raíz es 0.000043473.
4.- Hallar el valor de (2)^0.5 con precisión de 10^(-3), con el método de secante:
SOLUCION
Sea 2 un numero x, entonces debemos encontrar una función donde x= (2) ^0.5, esta función es x^2-2=y, si f(X)=0, entonces existe una raíz en dicho punto tal como se observa si grafica la función.
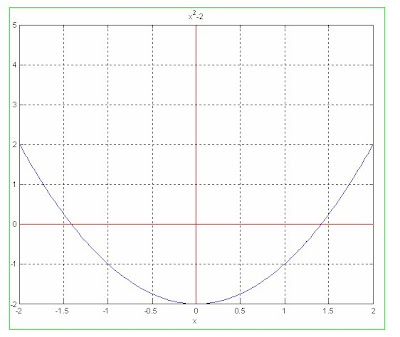
Empleando el método de la secante:
METODO DE SECANTE:
INGRESE LA FUNCION:
x^2-2
INGRESE EL PUNTO INICIAL X0:
0.5
INGRESE EL PUNTO INICIAL X1:
2
INGRESE TOLERANCIA:
10^(-3)
it x0 x1 x2 x2-x1
1 0.50000000 2.00000000 1.20000000 1.50000000
2 2.00000000 1.20000000 1.37500000 0.80000000
3 1.20000000 1.37500000 1.41747573 0.17500000
4 1.37500000 1.41747573 1.41416775 0.04247573
5 1.41747573 1.41416775 1.41421351 0.00330798
6 1.41416775 1.41421351 1.41421356 0.00004576
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.414213562
5.-hallar las raíces de la ecuación 3*x-2+exp(x)-x^2=0 con puntos iniciales de 0,1 con tolerancia 10^(-5). Usando el método de la secante.
SOLUCION
Graficamos para ver en que puntos se encuentran las raíces.
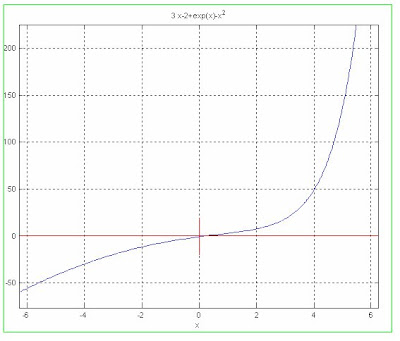
METODO DE SECANTE:
INGRESE LA FUNCION:
3*x-2+exp(x)-x^2
INGRESE EL PUNTO INICIAL X0:
0
INGRESE EL PUNTO INICIAL X1:
1
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x2 x2-x1
1 0.00000000 1.00000000 0.26894142 1.00000000
2 1.00000000 0.26894142 0.25717072 0.73105858
3 0.26894142 0.25717072 0.25753067 0.01177070
4 0.25717072 0.25753067 0.25753029 0.00035994
5 0.25753067 0.25753029 0.25753029 0.00000038
LA RAIZ BUSCADA ES= 0.257530285
6.-Hallar la raíces de la ecuación x^2+10*cos(x)=0, con puntos iniciales 1.5 ,2 con tolerancia de 10^(-5). Usando el método de la secante.
SOLUCION Graficando la función
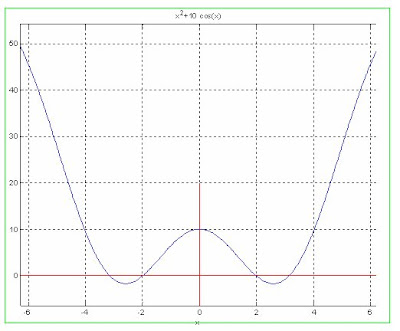
Se observa que tiene dos raíces, ero nos pide con los puntos iniciales de 1.5 y 2, lo que quiere decir, la raíz cercana a 2.
METODO DE SECANTE:
INGRESE LA FUNCION: x^2+10*cos(x)
INGRESE EL PUNTO INICIAL X0:1.5
INGRESE EL PUNTO INICIAL X1:2
INGRESE TOLERANCIA: 10^(-5)
it x0 x1 x2 x2-x1
1 1.50000000 2.00000000 1.97411404 0.50000000
2 2.00000000 1.97411404 1.96877850 0.02588596
3 1.97411404 1.96877850 1.96887321 0.00533554
4 1.96877850 1.96887321 1.96887294 0.00009472
5 1.96887321 1.96887294 1.96887294 0.00000028
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.968872938
7.- encuentre la raíz aproximada de x^3-x-1=0 en [1,2], con precisión de 10^(-5).
a) usando el método del secante.
b) usando el método de newton.
SOLUCION Graficando la función.
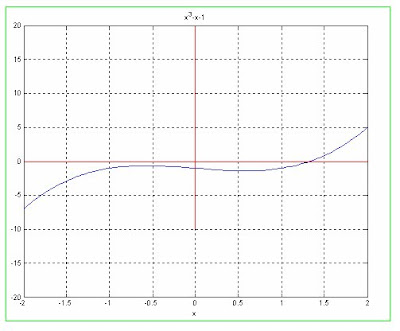
METODO DE SECANTE:
INGRESE LA FUNCION:
x^3-x-1
INGRESE EL PUNTO INICIAL X0:
1
INGRESE EL PUNTO INICIAL X1:
2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x2 x2-x1
1 1.00000000 2.00000000 1.16666667 1.00000000
2 2.00000000 1.16666667 1.25311203 0.83333333
3 1.16666667 1.25311203 1.33720645 0.08644537
4 1.25311203 1.33720645 1.32385010 0.08409441
5 1.33720645 1.32385010 1.32470794 0.01335635
6 1.32385010 1.32470794 1.32471797 0.00085784
7 1.32470794 1.32471797 1.32471796 0.00001003
8 1.32471797 1.32471796 1.32471796 0.00000001
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.324717957
METODO DE NEWTON:
INGRESE LA FUNCION:
x^3-x-1
INGRESE EL PUNTO INICIAL:
1
INGRESE TOLERANCIA:
10^(-5)
It x0 x1 x1-x0
1 1.000000000 1.500000000 0.500000000
2 1.500000000 1.347826087 0.152173913
3 1.347826087 1.325200399 0.022625688
4 1.325200399 1.324718174 0.000482225
5 1.324718174 1.324717957 0.000000217
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.324717957
8.- suponiendo que el crecimiento de una población esta determinada mediante la ecuación N(t)=Noe^(λt)+(υ/λ)( e^(λt)-1). Donde N(t) es el número de individuo en el tiempo (medido en años), λ es la razón de natalidad, No es la población inicial y υ es la razón constante de inmigración que se mide en numero de inmigraciones al año.
Supóngase que una población dada tiene 1000000 de individuos inicialmente y la constante de inmigración es de 435000 y se observa que al final del primer año la población es 1564000. ¿Determinar la razón de natalidad?
SOLUCION
Al final del primer año:
1564000=1000000(e)^(λ*1)+435000/λ((e)^(λ*1)-1)
Entonces:
Para encontrar el valor de razón de natalidad hacemos una función f(λ). Y encontremos la raíz de la ecuación.
1000000(e)^(λ*1)+435000/λ((e)^(λ*1)-1)-1564000=0
Graficando haciendo x=λ
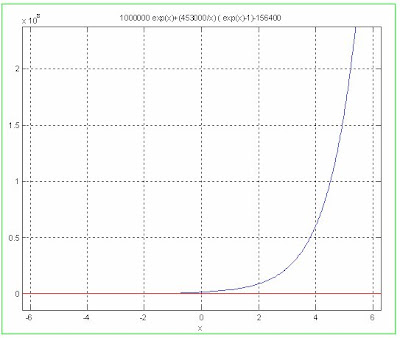
La razón de natalidad tiene el comportamiento que se muestra en la figura.
METODO DE NEWTON:
INGRESE LA FUNCION:
1000000*exp(x)+(453000/x)*( exp(x)-1)-156400
INGRESE EL PUNTO INICIAL:
1
INGRESE TOLERANCIA:
10^(-3)
it x0 x1 x1-x0
1 1.000000000 -0.053284974 1.053284974
2 -0.053284974 -1.109965138 1.056680164
3 -1.109965138 -2.121768318 1.011803180
4 -2.121768318 -2.949638477 0.827870159
5 -2.949638477 -3.392692810 0.443054333
6 -3.392692810 -3.485774102 0.093081291
7 -3.485774102 -3.489058779 0.003284677
8 -3.489058779 -3.489062659 0.000003880
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= -3.489062659
Entonces la razón de natalidad es 3.48 anual.
9.-hallar las raíces de la ecuación exp(x)-x-1=0, con punto inicial x0=0.5 con el método de newton modificado.
SOLUCION
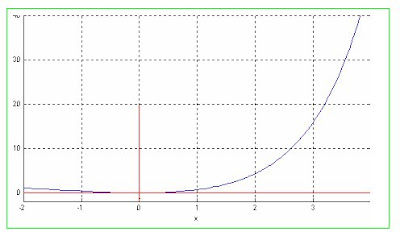
La raíz de la función esta dentro del intervalo de [-1,1].
METODO DE NEWTON MODIFICADO:
INGRESE LA FUNCION:
exp(x)-x-1
INGRESE EL PUNTO INICIAL:
0.5
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 0.500000000 -0.049299708 0.549299708
2 -0.049299708 -0.000398480 0.048901228
3 -0.000398480 -0.000000026 0.000398453
4 -0.000000026 -0.000000014 0.000000012
El proceso se completo satisfactoriamente:
La raíz buscada es= -0.000000014
10.- hallar las raíces de la ecuación x^4-4*x^2+4=0, con puntos iniciales 0,1, con tolerancia 10^(-6).
a) usando el método de newton
b) usando el método de newton modificado.
a) con el método de newton.
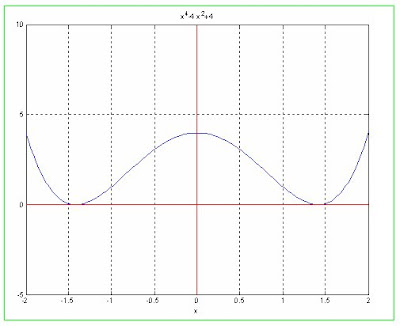
Se observa que en los intervalos de [-2,-1] y de [1,2], existen raíces.
Para la raíz positiva tenemos.
METODO DE NEWTON:
INGRESE LA FUNCION:
x^4-4*x^2+4
INGRESE EL PUNTO INICIAL:
2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 2.000000000 1.750000000 0.250000000
2 1.750000000 1.598214286 0.151785714
3 1.598214286 1.511509876 0.086704409
4 1.511509876 1.464427467 0.047082409
5 1.464427467 1.439750962 0.024676505
6 1.439750962 1.427095504 0.012655458
7 1.427095504 1.420683603 0.006411900
8 1.420683603 1.417455949 0.003227654
9 1.417455949 1.415836610 0.001619339
10 1.415836610 1.415025551 0.000811059
11 1.415025551 1.414619673 0.000405878
12 1.414619673 1.414416647 0.000203026
13 1.414416647 1.414315112 0.000101535
14 1.414315112 1.414264339 0.000050773
15 1.414264339 1.414238951 0.000025388
16 1.414238951 1.414226257 0.000012694
17 1.414226257 1.414219910 0.000006347
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.414219910
b).- con newton modificado.
METODO DE NEWTON MODIFICADO:
INGRESE LA FUNCION:
x^4-4*x^2+4
INGRESE EL PUNTO INICIAL:
2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 2.000000000 1.333333333 0.666666667
2 1.333333333 1.411764706 0.078431373
3 1.411764706 1.414211438 0.002446733
4 1.414211438 1.414213562 0.000002124
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.414213562
De los dos métodos empleados se puede obtener similares, lo más conveniente es emplear el método d newton modificado, ya que converge con mayor rapidez.
a.- método de la bisección
b.- método del punto fijo
c.- método de newton –Raphson
d.- método de la secante
e.- método de la falsa posición
f.- método de newton modificado
g.- entre otros métodos
1.- METODO DE LA BISECCION
Si se tiene dos puntos x1 y x2 entonces sus correspondiente imágenes son f(x1) y f(x2), lo que se quiere es que estas dos imágenes sean de singo contrario, para que en este intervalo de x1 a x2 se encuentra la raíz buscada. Geométricamente se tiene en la figura 1.

En esta figura 1 se observa que para x1, su imagen f(x1) negativo, para x2 su imagen f(x2) es positivo, entonces en el intervalo [x1, x2], se encuentra la raíz buscada.
Una vez que se ha localizado el intervalo en la cual se encuentra la raíz, solo nos queda
Aproximarnos. Geométricamente se interpreta así.

En la figura Nº 02, se ingresa inicialmente X1 y X2, luego se obtiene XM donde M1 corresponde a la mitad del intervalo [X1 X2], a continuación para acercarnos a la raíz.
Tomamos XM=X2 y X2=X2 y se obtiene el nuevo punto medio M2 que corresponde a la mitad del intervalo [XM, X2], y así sucesivamente hasta acercarnos a la raíz
PROGRAMA EN MATLAB PARA EL METODO DE BISECCION

2.- METODO DEL PUNTO FIJOEl método del punto fijo consiste en que a partir de un punto inicial nos acercamos a la raíz buscada, para lo cual se requiere hacer de la función principal f(x) igual a la siguiente expresión: f(x)=x-g(x).
Geométricamente el método del punto fijo consiste en lo siguiente:
Sabemos que existen dos funciones:
y=x,
y=g(x),
Además sabemos que cuando g’(x) <1, entonces el método converge y se puede encontrar la raíz buscada, tal como se muestra en las siguientes figuras Nº 03 y 04

A partir de X0 se llega a la raíz R, cuando esta converge, tal como se observa en la figura Nº 03.

Convergencia oscilatoria, según el número de iteraciones se aproxima a la raíz
PROGRAMA EN MATLAB PARA EL METODO DEL PUNTO FIJO

3.-METODO DE NEWTON RAPHSONEl método consiste en que a partir de un punto dado, la pendiente de la función tiene que converger a la raíz, geométricamente se interpreta de la siguiente manera

Por lo tanto para determinar la raíz mediante el método de newton es necesario dar valor inicial (X0) adecuada, para que pueda converger rápidamente. Como se observa en la Fig. Nº 05, dado un punto inicial se determina la ecuación de la recta que es tangente a la función en ese punto, luego con esta se determina un X1, que corresponde a la intersección de la ecuación lineal con el eje de las abscisas, con este valor nuevamente se determina la ecuación de la recta tangente a la función, y así sucesivamente nos acercamos a la raíz de la ecuación.
PROGRAMA EN MATLAB PARA EL METODO DE NEWTON RAPHSON

4.- METODO DE LA SECANTE.En el método de la secante no es necesario emplear la derivada de la función, por lo que es uno de los métodos utilizados cuando las derivadas son dificultosas, solo se requiere dos puntos iniciales, estos puntos deben ser dados con criterio para que pueda converger rápidamente.
Geométricamente este método consiste emplear una secante a la función dada.

Para este método inicialmente se tiene los puntos Xo y X1, con las correspondientes imágenes de estos dos puntos se determina la ecuación de la recta secante a la función dada, luego esta se intercepta con el eje de las abscisas obteniendo un punto X3, la imagen de X3 para la siguiente iteración es nuevo X1 para definir la secante a la función e interceptar al eje de las abscisas, así nos acercamos cada vez mas hacia a la raíz buscada
PROGRAMA EN MATLAB PARA EL METODO DE LA SECANTE

5.-METODO DE NEWTON MODOFICADOLos criterios que se toman son las tomadas en el método de newton Raspón.
PROGRAMA EN MATLAB PARA EL METODO DE NEWTON MODIFICADO.

6.- METODO DE FALSA POSICIONEl método de la falsa posición también requiere dos puntos iniciales, donde sus correspondientes imágenes deben ser de signos contrarios así como en el método de la bisección, para entender este método se ilustra geométricamente.
Para los puntos X0 y X1 se determina sus correspondientes imágenes, estos deben ser de signo contrario, así como se muestra en la Fig. Nº 07, se define la ecuación de esta recta, para poder interceptar con el eje de las abscisas, este punto de intersección tiene una imagen que puede ser positivo o negativo, si es positivo como en el grafico que se ilustra x2 es X0 para la siguiente iteración y X1 sigue siendo X1, como se observa cada vez nos acercamos ala raíz. Se continúa con el mismo proceso hasta satisfacer una determinada tolerancia.

PROGRAMA EN MATLAB PARA EL METODO DE FALSA POSICION

EJERCICIOS RESUELTOS
1.-Hallar las raíces de las funciones dadas a continuación intervalos dados y con una precisión de 10^ (-4).
a) x^3-2*x-5=0 en [1, 4]
b) x-0.8-0.2*sin(x)=0 en [0, pi/2]
SOLUCIÓN
a)
Empleando el método de newton.
Para lo cual graficamos inicialmente para aproximar en que punto se encuentra la raíz

Como se indicaba en la pregunta existe una raíz en ese intervalo, por la tanto:
METODO DE NEWTON:
INGRESE LA FUNCION:
x^3-2*x-5
INGRESE EL PUNTO INICIAL:
1
INGRESE TOLERANCIA:
10^(-4)
it x0 x1 |x1-x0|
1 1.000000000 7.000000000 6.000000000
2 7.000000000 4.765517241 2.234482759
3 4.765517241 3.348702759 1.416814482
4 3.348702759 2.531599641 0.817103118
5 2.531599641 2.173915885 0.357683756
6 2.173915885 2.097883686 0.076032198
7 2.097883686 2.094557716 0.003325971
8 2.094557716 2.094551482 0.000006234
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 2.094551482
b)
Graficando

La raíz se encuentra en el intervalo [0,2], entonces.
INGRESE LA FUNCION:
x-0.8-0.2*sin(x)
INGRESE EL PUNTO INICIAL:
>> 0
INGRESE TOLERANCIA:
10^ (-4)
it x0 x1 |x1-x0|
1 0.000000000 1.000000000 1.000000000
2 1.000000000 0.964452968 0.035547032
3 0.964452968 0.964333889 0.000119079
4 0.964333889 0.964333888 0.000000001
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 0.964333888
2.- la función f(x)= (4*x-7)/(x-2) tiene una raíz en p=1.75. Graficar la función f(x). Use el método de newton con los siguientes puntos iniciales.
a) x0=1.625 b) x0=1.875
c) x0=1.5 d) x0=1.95
e) x0=3 f) x0=7 Explique sus resultados.
SOLUCION

En el grafico de la función se observa que existe una raíz en ese punto, a continuación probaremos con cada uno de los puntos:
Para x0=1.625
INGRESE LA FUNCION:
(4*x-7)/(x-2)
INGRESE EL PUNTO INICIAL:
1.625
INGRESE TOLERANCIA:
10^(-4)
it x0 x1 x1-x0
1 1.625000000 1.812500000 0.187500000
2 1.812500000 1.765625000 0.046875000
3 1.765625000 1.750976563 0.014648438
4 1.750976563 1.750003815 0.000972748
5 1.750003815 1.750000000 0.000003815
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.750000000
Resultados:
X0 Raíz
1.625 1.75
1.875 1.75
1.5 NaN
1.95 1.75
3 NaN
7 NaN
Para los puntos 1.5, 3 y 7, se obtiene como resultado NaN, matlab quiere decir que es u número infinito, dado que en esos puntos la tangente a la función se hacen grandes y divergen de la raíz.
3.- use el método de newton para resolver la ecuación
(sin(x)-x)^2=0 con una presicion de 10^(-5)
a) x0= pi/2
b) x0=5*pi
c) x0=10*pi
SOLUCION
Graficando la función se tiene.

Existe la posibilidad de que haya raíz en el intervalo de [-1 1]. Entonces para cada caso realizamos las iteraciones correspondientes.
INGRESE LA FUNCION:
(sin(x)-x)^2
INGRESE EL PUNTO INICIAL:
pi/2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 1.570796327 1.285398163 0.285398163
2 1.285398163 1.058629574 0.226768589
3 1.058629574 0.875326162 0.183303413
4 0.875326162 0.725607891 0.149718271
5 0.725607891 0.602510190 0.123097701
6 0.602510190 0.500860754 0.101649436
7 0.500860754 0.416679618 0.084181136
8 0.416679618 0.346828593 0.069851025
9 0.346828593 0.288791050 0.058037543
10 0.288791050 0.240525001 0.048266048
11 0.240525001 0.200360036 0.040164965
12 0.200360036 0.166921948 0.033438088
13 0.166921948 0.139075759 0.027846189
14 0.139075759 0.115881511 0.023194248
15 0.115881511 0.096559276 0.019322234
16 0.096559276 0.080461060 0.016098216
17 0.080461060 0.067047989 0.013413071
18 0.067047989 0.055871649 0.011176340
19 0.055871649 0.046558739 0.009312911
20 0.046558739 0.038798388 0.007760351
21 0.038798388 0.032331666 0.006466723
22 0.032331666 0.026942867 0.005388799
23 0.026942867 0.022452281 0.004490586
24 0.022452281 0.018710171 0.003742110
25 0.018710171 0.015591773 0.003118398
26 0.015591773 0.012993123 0.002598650
27 0.012993123 0.010827590 0.002165533
28 0.010827590 0.009022985 0.001804605
29 0.009022985 0.007519150 0.001503835
30 0.007519150 0.006265956 0.001253194
31 0.006265956 0.005221629 0.001044327
32 0.005221629 0.004351356 0.000870272
33 0.004351356 0.003626130 0.000725227
34 0.003626130 0.003021775 0.000604355
35 0.003021775 0.002518145 0.000503629
36 0.002518145 0.002098454 0.000419691
37 0.002098454 0.001748712 0.000349742
38 0.001748712 0.001457260 0.000291452
39 0.001457260 0.001214383 0.000242877
40 0.001214383 0.001011986 0.000202397
41 0.001011986 0.000843322 0.000168664
42 0.000843322 0.000702768 0.000140554
43 0.000702768 0.000585640 0.000117128
44 0.000585640 0.000488033 0.000097607
45 0.000488033 0.000406694 0.000081339
46 0.000406694 0.000338912 0.000067782
47 0.000338912 0.000282427 0.000056485
48 0.000282427 0.000235356 0.000047071
49 0.000235356 0.000196130 0.000039226
50 0.000196130 0.000163441 0.000032688
LA RAIZ BUSCADA ES= 0.000163441
Se observa que requiere muchas iteraciones.
X0 Raíz Número de it
Pi/2=1.700796 0.000163441 50
5*pi=15.707963 0.000507692 50
10*pi=31.4159265 NaN
Si se sigue buscado un punto que satisfaga mejor nuestro búsqueda de raíz seria un numero cercano a cero, dado que la función no corta al eje de la abscisas, solo intercepta en x=0. Se puede observar cuando mas cerca es el punto inicial nos aproximamos la raíz, la raíz buscada con la precisión dada varia de acuerdo al punto inicial. Así para X1= 0.002, la raíz es 0.000043473.
4.- Hallar el valor de (2)^0.5 con precisión de 10^(-3), con el método de secante:
SOLUCION
Sea 2 un numero x, entonces debemos encontrar una función donde x= (2) ^0.5, esta función es x^2-2=y, si f(X)=0, entonces existe una raíz en dicho punto tal como se observa si grafica la función.

Empleando el método de la secante:
METODO DE SECANTE:
INGRESE LA FUNCION:
x^2-2
INGRESE EL PUNTO INICIAL X0:
0.5
INGRESE EL PUNTO INICIAL X1:
2
INGRESE TOLERANCIA:
10^(-3)
it x0 x1 x2 x2-x1
1 0.50000000 2.00000000 1.20000000 1.50000000
2 2.00000000 1.20000000 1.37500000 0.80000000
3 1.20000000 1.37500000 1.41747573 0.17500000
4 1.37500000 1.41747573 1.41416775 0.04247573
5 1.41747573 1.41416775 1.41421351 0.00330798
6 1.41416775 1.41421351 1.41421356 0.00004576
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.414213562
5.-hallar las raíces de la ecuación 3*x-2+exp(x)-x^2=0 con puntos iniciales de 0,1 con tolerancia 10^(-5). Usando el método de la secante.
SOLUCION
Graficamos para ver en que puntos se encuentran las raíces.

METODO DE SECANTE:
INGRESE LA FUNCION:
3*x-2+exp(x)-x^2
INGRESE EL PUNTO INICIAL X0:
0
INGRESE EL PUNTO INICIAL X1:
1
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x2 x2-x1
1 0.00000000 1.00000000 0.26894142 1.00000000
2 1.00000000 0.26894142 0.25717072 0.73105858
3 0.26894142 0.25717072 0.25753067 0.01177070
4 0.25717072 0.25753067 0.25753029 0.00035994
5 0.25753067 0.25753029 0.25753029 0.00000038
LA RAIZ BUSCADA ES= 0.257530285
6.-Hallar la raíces de la ecuación x^2+10*cos(x)=0, con puntos iniciales 1.5 ,2 con tolerancia de 10^(-5). Usando el método de la secante.
SOLUCION Graficando la función

Se observa que tiene dos raíces, ero nos pide con los puntos iniciales de 1.5 y 2, lo que quiere decir, la raíz cercana a 2.
METODO DE SECANTE:
INGRESE LA FUNCION: x^2+10*cos(x)
INGRESE EL PUNTO INICIAL X0:1.5
INGRESE EL PUNTO INICIAL X1:2
INGRESE TOLERANCIA: 10^(-5)
it x0 x1 x2 x2-x1
1 1.50000000 2.00000000 1.97411404 0.50000000
2 2.00000000 1.97411404 1.96877850 0.02588596
3 1.97411404 1.96877850 1.96887321 0.00533554
4 1.96877850 1.96887321 1.96887294 0.00009472
5 1.96887321 1.96887294 1.96887294 0.00000028
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.968872938
7.- encuentre la raíz aproximada de x^3-x-1=0 en [1,2], con precisión de 10^(-5).
a) usando el método del secante.
b) usando el método de newton.
SOLUCION Graficando la función.

METODO DE SECANTE:
INGRESE LA FUNCION:
x^3-x-1
INGRESE EL PUNTO INICIAL X0:
1
INGRESE EL PUNTO INICIAL X1:
2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x2 x2-x1
1 1.00000000 2.00000000 1.16666667 1.00000000
2 2.00000000 1.16666667 1.25311203 0.83333333
3 1.16666667 1.25311203 1.33720645 0.08644537
4 1.25311203 1.33720645 1.32385010 0.08409441
5 1.33720645 1.32385010 1.32470794 0.01335635
6 1.32385010 1.32470794 1.32471797 0.00085784
7 1.32470794 1.32471797 1.32471796 0.00001003
8 1.32471797 1.32471796 1.32471796 0.00000001
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.324717957
METODO DE NEWTON:
INGRESE LA FUNCION:
x^3-x-1
INGRESE EL PUNTO INICIAL:
1
INGRESE TOLERANCIA:
10^(-5)
It x0 x1 x1-x0
1 1.000000000 1.500000000 0.500000000
2 1.500000000 1.347826087 0.152173913
3 1.347826087 1.325200399 0.022625688
4 1.325200399 1.324718174 0.000482225
5 1.324718174 1.324717957 0.000000217
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.324717957
8.- suponiendo que el crecimiento de una población esta determinada mediante la ecuación N(t)=Noe^(λt)+(υ/λ)( e^(λt)-1). Donde N(t) es el número de individuo en el tiempo (medido en años), λ es la razón de natalidad, No es la población inicial y υ es la razón constante de inmigración que se mide en numero de inmigraciones al año.
Supóngase que una población dada tiene 1000000 de individuos inicialmente y la constante de inmigración es de 435000 y se observa que al final del primer año la población es 1564000. ¿Determinar la razón de natalidad?
SOLUCION
Al final del primer año:
1564000=1000000(e)^(λ*1)+435000/λ((e)^(λ*1)-1)
Entonces:
Para encontrar el valor de razón de natalidad hacemos una función f(λ). Y encontremos la raíz de la ecuación.
1000000(e)^(λ*1)+435000/λ((e)^(λ*1)-1)-1564000=0
Graficando haciendo x=λ

La razón de natalidad tiene el comportamiento que se muestra en la figura.
METODO DE NEWTON:
INGRESE LA FUNCION:
1000000*exp(x)+(453000/x)*( exp(x)-1)-156400
INGRESE EL PUNTO INICIAL:
1
INGRESE TOLERANCIA:
10^(-3)
it x0 x1 x1-x0
1 1.000000000 -0.053284974 1.053284974
2 -0.053284974 -1.109965138 1.056680164
3 -1.109965138 -2.121768318 1.011803180
4 -2.121768318 -2.949638477 0.827870159
5 -2.949638477 -3.392692810 0.443054333
6 -3.392692810 -3.485774102 0.093081291
7 -3.485774102 -3.489058779 0.003284677
8 -3.489058779 -3.489062659 0.000003880
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= -3.489062659
Entonces la razón de natalidad es 3.48 anual.
9.-hallar las raíces de la ecuación exp(x)-x-1=0, con punto inicial x0=0.5 con el método de newton modificado.
SOLUCION

La raíz de la función esta dentro del intervalo de [-1,1].
METODO DE NEWTON MODIFICADO:
INGRESE LA FUNCION:
exp(x)-x-1
INGRESE EL PUNTO INICIAL:
0.5
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 0.500000000 -0.049299708 0.549299708
2 -0.049299708 -0.000398480 0.048901228
3 -0.000398480 -0.000000026 0.000398453
4 -0.000000026 -0.000000014 0.000000012
El proceso se completo satisfactoriamente:
La raíz buscada es= -0.000000014
10.- hallar las raíces de la ecuación x^4-4*x^2+4=0, con puntos iniciales 0,1, con tolerancia 10^(-6).
a) usando el método de newton
b) usando el método de newton modificado.
a) con el método de newton.

Se observa que en los intervalos de [-2,-1] y de [1,2], existen raíces.
Para la raíz positiva tenemos.
METODO DE NEWTON:
INGRESE LA FUNCION:
x^4-4*x^2+4
INGRESE EL PUNTO INICIAL:
2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 2.000000000 1.750000000 0.250000000
2 1.750000000 1.598214286 0.151785714
3 1.598214286 1.511509876 0.086704409
4 1.511509876 1.464427467 0.047082409
5 1.464427467 1.439750962 0.024676505
6 1.439750962 1.427095504 0.012655458
7 1.427095504 1.420683603 0.006411900
8 1.420683603 1.417455949 0.003227654
9 1.417455949 1.415836610 0.001619339
10 1.415836610 1.415025551 0.000811059
11 1.415025551 1.414619673 0.000405878
12 1.414619673 1.414416647 0.000203026
13 1.414416647 1.414315112 0.000101535
14 1.414315112 1.414264339 0.000050773
15 1.414264339 1.414238951 0.000025388
16 1.414238951 1.414226257 0.000012694
17 1.414226257 1.414219910 0.000006347
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.414219910
b).- con newton modificado.
METODO DE NEWTON MODIFICADO:
INGRESE LA FUNCION:
x^4-4*x^2+4
INGRESE EL PUNTO INICIAL:
2
INGRESE TOLERANCIA:
10^(-5)
it x0 x1 x1-x0
1 2.000000000 1.333333333 0.666666667
2 1.333333333 1.411764706 0.078431373
3 1.411764706 1.414211438 0.002446733
4 1.414211438 1.414213562 0.000002124
El proceso se completo satisfactoriamente:
LA RAIZ BUSCADA ES= 1.414213562
De los dos métodos empleados se puede obtener similares, lo más conveniente es emplear el método d newton modificado, ya que converge con mayor rapidez.
Suscribirse a:
Comentarios (Atom)


