SOLUCION
PROGRAMA EN MATLAB PARA APROXIMAR A UNA RECTA.
function correl
xi=input('ingrese los valores de xi:\n');
yi=input('ingreso los valores de yi:\n');
n=length(xi);
A=ones(2);
for i=1:2
for j=1:2
A(i,j)=sum(xi.^(1+i-j));
end
end
B=ones(2,1);
for i=0:1
B(1+i,1)=sum(yi.*xi.^i);
end
X=inv(A)*(B);
l=X(1);r=X(2);
fprintf('\nLos coeficientes de la ecuacion son:\n')
fprintf(' a b\n')
fprintf('%8.5f%10.5f\n',l,r)
y=l*xi+r;
m=sum(yi)/n;
t=sum((yi-y).^2);
j=sum((yi-m).^2);
r2=1-(t/j);
z=(r2)^0.5;
fprintf('\n El coeficiente de determinacion r^2=');
fprintf('%5.5f\n',r2);
if(l>0)
fprintf('\n El coeficiente de correlacion r=');
fprintf('%5.5f\n',z);
else
fprintf('\n El coeficiente de correlacion r=');
fprintf('%5.5f\n',-z);
end
x1=xi;
x1=sort(x1);
x1=x1(1):0.001:x1(n);
p=polyval(X,x1);
plot(xi,yi,'m.',x1,p),grid on
2.-hallar la recta por el método de los mínimos cuadrados que se ajusten mejor al conjunto de datos. Escribir las ecuaciones normales.
xi 4 5 2 5 6 7 1 8 3 7
yi 5 6 4 5 7 10 3 11 4 9
SOLUCION
Empleando el programa de la pregunta 1.
Graficando:
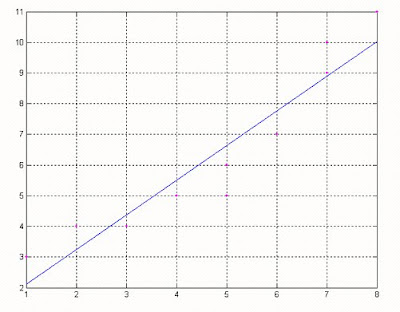
y los resultados de la ecuación de la recta y su coeficiente de correlación son:
correl
ingrese los valores de xi:
[4 5 2 5 6 7 1 8 3 7]
ingreso los valores de yi:
[5 6 4 5 7 10 3 11 4 9]
Los coeficientes de la ecuacion son:
a b
1.13025 0.97479
El coeficiente de determinacion r^2=0.88900
El coeficiente de correlacion r=0.94287
3.-dado el conjunto de datos:
xi Yi
0.15 4.4964
0.40 5.1284
0.60 5.6931
1.01 6.2884
1.50 7.0989
2.20 7.5507
2.4 7.5106
2.70 8.0756
2.90 7.8708
3.50 8.2408
3.80 8.5303
4.40 8.7394
4.60 8.9981
5.10 9.1450
6.60 9.5070
7.60 9.9115
Se ajusta a la función y=bx^a.
a).-linealizar y=bx^a y modifique el programa de mínimos cuadrados para obtener esta función.
b).- hacer en la misma pantalla grafica de la función en el plano xy y la grafica en el plano log(x) log(y)).
SOLUCION.
a.- linealizando se tiene:
ln(y)=ln(b)+a*ln(x),
Luego para que sea lineal
y=a1*x+b1
Entonces:
a1=a; b1=b; ln(y)=y; ln(x)=x.
Modificando el programa en matlab para estas expresiones: se ha guardado con el nombre de “bxn”.
bxn
ingrese los valores de xi:
[0.15 0.40 0.6 1.01 1.5 2.2 2.4 2.7 2.9 3.5 3.8 4.4 4.6 5.1 6.6 7.6]
ingreso los valores de yi:
[4.4964 5.1284 5.6931 6.2884 7.0989 7.5507 7.5106 8.0756 7.8708 8.2403 8.5303 8.7394 8.9981 9.1450 9.5070 9.9115]
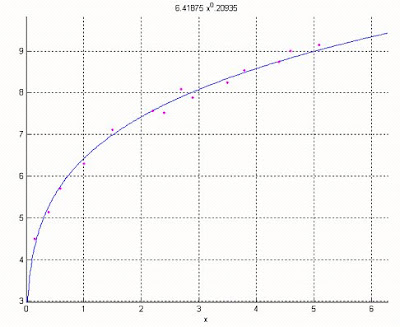
Los coeficientes de la ecuacion son:
a b
0.20935 6.41575
La función y=6.41875*x^0.20935
El coeficiente de determinacion r^2=0.99314
El coeficiente de correlación r=1.85876
4.- escribir un programa para aproximar por polinomio P(x) de grado k un conjunto de datos por el método de los mínimos cuadrados, incluir en dicho programa la grafica del polinomio, grafica del conjunto de datos el coeficiente de correlación.
PROGRAMA PARA APROXIMAR A UN POLINOMIO DE GRADO K.
function polinomial
fprintf('\n FUNCION POLINOMIAL \n')
x=input('\n Ingrese los valores de xi :\n');
y=input('\n Ingrese los valores de yi :\n');
n=input('\n Ingrese el grado del polinomio:\n');
m=n+1;
A=ones(m);
for i=1:m
for j=1:m
A(i,j)=sum(x.^(n+i-j));
end
end
B=ones(m,1);
for i=0:n
B(1+i,1)=sum(y.*x.^i);
end
Z=(inv(A)*B);
fprintf('los coeficientes del polinomio son:\n');
fprintf('%8.5f\n',Z);
x1=x;
x1=sort(x1);
x1=x1(1):0.001:x1(length(x1));
H=polyval(Z,x1);
S=polyval(Z,x);
L=sum(y)/length(y);
R=sum((y-S).^2);
C=sum((y-L).^2);
K=1-(R/C);
J=K^0.5;
fprintf('El coeficiente de determinacion r^2:\n');
fprintf('%8.5f\n',K);
fprintf('El coeficiente de correlacion r:\n');
fprintf('%8.5f\n',J);
plot(x,y,'r*',x1,H),grid on
5.- Obtener la parábola por el método de los mínimos cuadrados que se aproxime ala función f(x)=x^(1/3) en los puntos 1,0,8, ¿Cuáles son las ecuaciones normales, interprete el coeficiente de correlación.
SOLUCION
Debemos aproximar este conjunto de valores a una ecuación de segundo grado.
El conjunto de datos seran:
Xi Yi
-1 -1
0 0
8 2
Empleando el programa polinomial.
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-1 0 8]
Ingrese los valores de yi :
[-1 0 2]
Ingrese el grado del polinomio:
2
los coeficientes del polinomio son:
-0.08333
0.91667
-0.00000
El coeficiente de determinacion r^2:
1.00000
El coeficiente de correlación r:
1.00000
El coeficiente de correlación r es 1, dado que todos los puntos pasan por la ecuación de la parábola
F(x)=-0.0833*x^2+0.91667*x=-1/12*x^2+11/12*x
6.-si una población tiene un crecimiento logístico y no puede superar la cantidad de 1000 individuos entonces el número P de individuos t viene dado por:
P(t)=1000/(1+Ce^At)
Aproxime mediante el método de los mínimos cuadrados, con linealizacion el valor C y A para los siguientes datos:
Xi 0 1 2 3 4
yi 200 300 650 850 950
Solución
Linealizando la función P(x), se tiene:
Ln(1000/y-1)=At+ln(C),
Entonces:
y=ln(1000/y-1); x=x; A=a; C=exp(b)
Modificando el programa de correl se tiene:
ingrese los valores de xi:
[0 1 2 3 4]
ingreso los valores de yi:
[200 400 650 850 950]
Los coeficientes de la ecuación son:
A C
-1.08015 4.30184
7.- considere los puntos {(-2,-3), (-1,-6), (0,-5), (1,1), (2,13)}
a.- determinar el polinomio de grado 3 por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales el coeficiente de correlación
Solución:
Para un polinomio de tercer grado:
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
3
los coeficientes del polinomio son:
0.16667
2.50000
3.33333
-5.00000
El coeficiente de determinacion r^2:
1.00000
El coeficiente de correlación r:
1.00000
Entonces el polinomio de grado tres es:
0.16667*x^3+2.5*x^2+3.3333*x-5.0
b.-determine la parábola por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales el coeficiente de correlación.
Solución
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
2
los coeficientes del polinomio son:
2.50000
3.90000
-5.00000
El coeficiente de determinacion r^2:
0.99833
El coeficiente de correlación r= 0.99917
Entonces la función parabólica es:
Y=2.5*x^2+3.9*x-5
c.- determinar la recta por el método de mínimos cuadrados que se ajuste a los datos, indicar las ecuaciones normales, coeficiente de correlación.
Solución
FUNCION POLINOMIAL
Ingrese los valores de xi :
[-2 -1 0 1 2]
Ingrese los valores de yi :
[-3 -6 -5 1 13]
Ingrese el grado del polinomio:
1
Los coeficientes del polinomio son:
3.90000
0.00000
El coeficiente de determinacion r^2:
0.63375
El coeficiente de correlación r:
0.79608
De donde se tiene la recta:
Y=3.9*x
d.- explicar los resultados.
Los puntos dados se ajustan mejor a la un polinomio de tercer grado, dado que todos los puntos pasan por la grafica de la función, así como explica sus coeficientes de correlación, para tercer grado es 1.00 y es la recta la que mejor se aproximan los puntos, por ello su coeficiente de correlación es 0.79608.


